Conceptual Fields, Problem Solving and Intelligent Computer Tools
Gérard Vergnaud
Zu finden in: Computer-Based Learning Environments and Problem Solving (Seite 287 bis 308), 1992
 Diese Seite wurde seit 7 Jahren inhaltlich nicht mehr aktualisiert.
Unter Umständen ist sie nicht mehr aktuell.
Diese Seite wurde seit 7 Jahren inhaltlich nicht mehr aktualisiert.
Unter Umständen ist sie nicht mehr aktuell.
 Zusammenfassungen
Zusammenfassungen
 The goal of this paper is to present an overview of the theory of conceptual fields, illustrated by the examples of additive structures and multiplicative structures. The main difficulties encountered by students in learning mathematics and other scientific topics are conceptual. These difficulties cannot be analysed if student´s conceptions are investigated independently of the schemes that organize their behavior in problem solving situations, and if a concept or a class of situations is examined in isolation. A conceptual field can be defined as both a set of classes of situations, and as a set of interconnected concepts. This paper presents a theoretical analysis of the relationship between explicit knowledge and the implicit operational invariants that underlie schemes. Examples of theorems-in-action and of the relationships between concepts and symbolic representations are presented, as well as ways of using the framework of conceptual fields to devise intelligent computer tools.
The goal of this paper is to present an overview of the theory of conceptual fields, illustrated by the examples of additive structures and multiplicative structures. The main difficulties encountered by students in learning mathematics and other scientific topics are conceptual. These difficulties cannot be analysed if student´s conceptions are investigated independently of the schemes that organize their behavior in problem solving situations, and if a concept or a class of situations is examined in isolation. A conceptual field can be defined as both a set of classes of situations, and as a set of interconnected concepts. This paper presents a theoretical analysis of the relationship between explicit knowledge and the implicit operational invariants that underlie schemes. Examples of theorems-in-action and of the relationships between concepts and symbolic representations are presented, as well as ways of using the framework of conceptual fields to devise intelligent computer tools. Dieses Kapitel erwähnt ...
Dieses Kapitel erwähnt ...
 Begriffe KB IB clear |  Computer Computer computer
, computer
,  Mathematik Mathematik mathematics
, mathematics
,  Problemlösefähigkeit Problemlösefähigkeit problem solving skills
, problem solving skills
,  Repräsentationstrias / EIS-Prinzip
, Repräsentationstrias / EIS-Prinzip
, 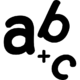 symbolische Repräsentation symbolische Repräsentation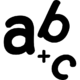 symbolic representation symbolic representation
|
 Dieses Kapitel erwähnt vermutlich nicht ...
Dieses Kapitel erwähnt vermutlich nicht ... 
 Nicht erwähnte Begriffe | enaktive Repräsentation, ikonische Repräsentation |
 Tagcloud
Tagcloud
 Anderswo finden
Anderswo finden
 Anderswo suchen
Anderswo suchen 
 Beat und dieses Kapitel
Beat und dieses Kapitel
Beat hat Dieses Kapitel während seiner Zeit am Institut für Medien und Schule (IMS) ins Biblionetz aufgenommen. Beat besitzt weder ein physisches noch ein digitales Exemplar. Aufgrund der wenigen Einträge im Biblionetz scheint er es nicht wirklich gelesen zu haben. Es gibt bisher auch nur wenige Objekte im Biblionetz, die dieses Werk zitieren.










 Biblionetz-History
Biblionetz-History